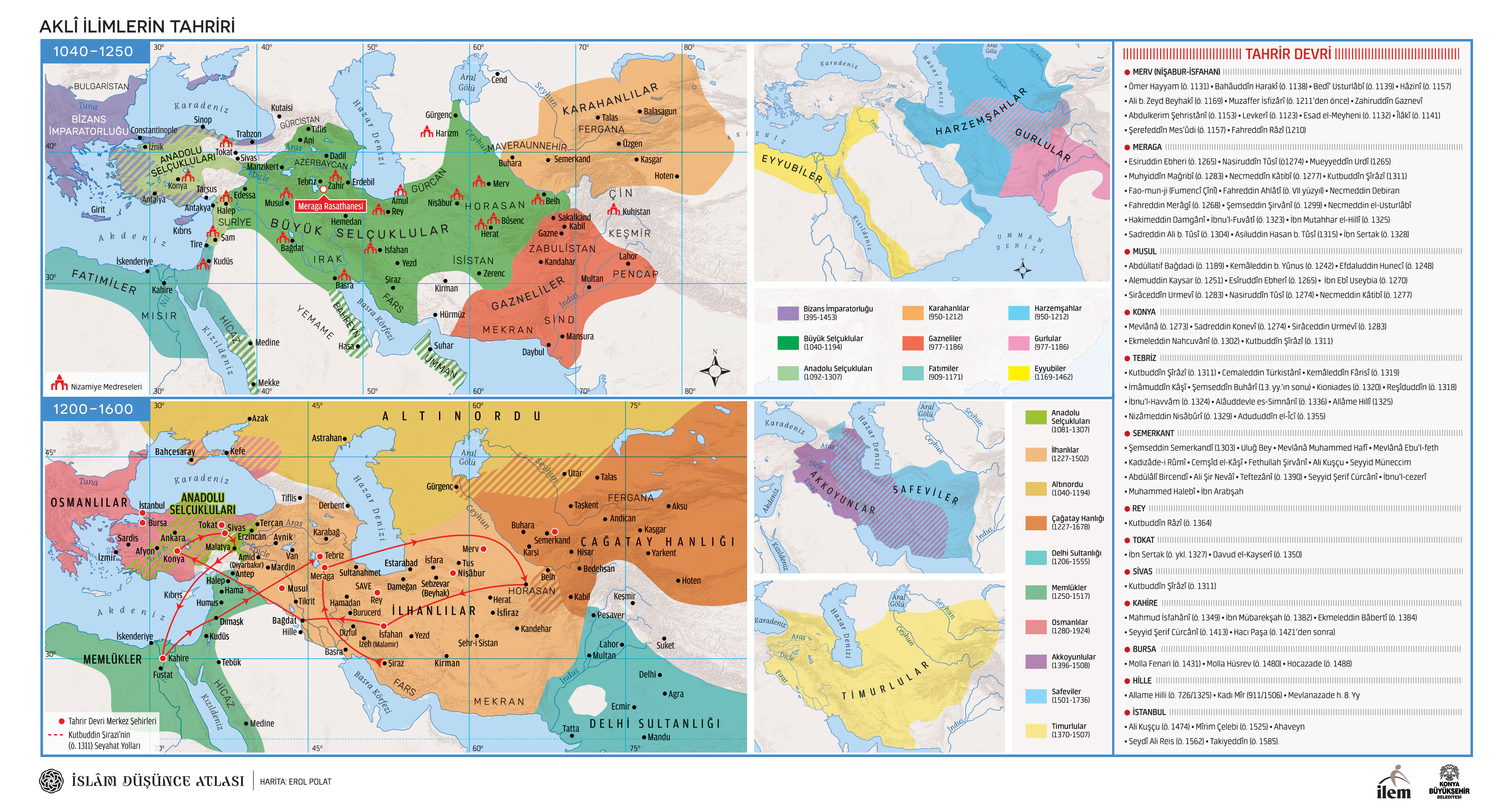
XI. yüzyılın hemen başında İslâm medeniyetinin Dâru'l-İslâm olması coğrafî değil daha çok manevî bir anlam ifade ediyordu. Her açıdan parçalanmışlık Büyük Selçuklu Devleti'nin kuruluşu (1040) ile bir nebze giderildi ve bu durum özellikle Doğu İslâm dünyasına kısmî bir birlik getirdi. Başka nedenler yanında Selçukluların merkez-çevre anlayışına dayalı siyâsî yaklaşımlarının etkisini taşıyan medreselerin bir öğretim kurumu olarak devlet eliyle yükselmesi Doğu İslam coğrafyasında, zamanla ortak eğitim ve öğretimden geçenler arasında ortak bir akıl, dil ve vicdan birliği oluşturdu; ayrıca bilginler yanında belirli bir eğitim almış, okuma-yazma bilen tahsilli insanlar sınıfının ortaya çıkmasına neden oldu. Anadolu, Suriye ve Filistin bölgelerinde Haçlı seferlerinin başlaması, Mısır'ın artık çökmeye yüz tutan Fâtimîler’in elinde bulunması, Endülüs ve Mağrib'te daha çok Aristotelesçi bir yaklaşımın baskın olması yanında Sultan Melikşâh'ın 1092 tarihinde ölmesinin akabinde Büyük Selçuk Devleti'nin parçalanma sürecine girmesi, daha da önemlisi hem iç sorunlar hem de Batı Avrupa'daki gelişmeler sebebiyle uluslararası ticâretteki hakimiyetin zayıflaması gibi maddî ve manevî nedenler, Dâru'l-İslâm'daki matematik bilimlerdeki ilmî hareketin ritminin yavaşça Bağdâd ve çevresinden daha Doğu'ya, önce İsfehân, Rey, Nîşâbûr gibi İran şehirlerine akabinde de merkezi Merv olan Türkistân coğrafyasına kaymasına neden oldu.

1097-1118 tarihleri arasında yaklaşık 21 yıl boyunca Horasan Selçuklu sultanı olan Sencer, 1118-1157 tarihleri arasında da Büyük Selçuklu sultanı olarak 39 yıl, toplamda 60 yıl hükümdarlık yaptı. Başta babası Sultan Melikşâh'ın bıraktığı miras olmak üzere tüm Selçuklu coğrafyasındaki birikimi, yarattığı bilgi için zorunlu olan istikrâr ortamında bir araya getirdi ve kanaatimizce Matematik bilimler için Bağdâd'dan sonra Merv merkezli en önemli ilim ve kültür hareketini örgütledi ve himâye etti. Burada, Ömer Hayyâm, Bahâuddin Harakî, Bedîʻ Usturlâbî, Hubûbî, Hâzinî, Ebû Saîd Urmevî, Ebû'l-Kâsım Nîsâbûrî, Esad Beyhâkî, İbn Melka, Muzaffer İsfizârî, Muhammed Beyhâkî, Zâhiruddin Gaznevî, Hüseyin Semerkandî gibi yalnızca matematik bilimlerde eser veren onlarca âlimin olduğu ve adında 'Sencerî' sözcüğü bulunan onlarca eser yazıldığı görülür. Bu çizgi, Sultan Sencer sonrası Harzemşâhlar döneminde de devam etti ve başta Fahreddin Râzî, Şerefuddin Mesûdî, Şemseddin Çağmînî, Hubeyş Tiflîsî, Esîrüddin Ebherî, Hüsâmeddin Sâlâr, Abdülmelik Şîrâzî, Mesûd Kazerûnî, Şemseddin Semerkandî gibi daha sonra –önce Türkistân'daki istikrarsız ortamdan akabinde de Moğol işgalinden uzaklaşarak– İran, Kafkasya, Mısır ve Anadolu coğrafyasına doğru yola çıkan onlarca önemli ismi yetiştirdi.

Pek çok maddî ve manevî şartın bir araya gelmesi, sosyo-ekonomik ve politik koşulların uygunluğu yanında Gazalî'nin hem mantık hem de matematik için sağladığı entelektüel meşrûiyet, bu dönemde ve bu coğrafyada, mantık esaslı felsefe için tahkîk ve tal‘îm(matematik) esaslı felsefe için de tahrîr yöntemlerinin varlığa gelmesini sağladı; çünkü mantık ilminin meşrûiyeti tahkîk yöntemi için olmaz-ise-olmaz bir koşul iken, mefhûm itibariyle ta‘lîmî(matematiksel) olanın meşrûiyeti de tüm matematik bilimler için kalkışılacak tahrîr, yani bir ilme ait sorunları(meâsil) ve bu sorunlara ilişkin kanıtları(delâil) gereksiz olan her şeyden arındırıp sağınlaştırmak için olmaz-ise-olmaz bir şarttı. Bu çerçevede ilk tahrîr hareketinin konusunun, kadîm Matematik bilimlerinin en gelişmiş üyesi ve Mantık ile akraba Hendeseyi temsil eden Eukleides'in Elemanlar'ı olması bir tesadüf değildir. Nitekim Sultan Sencer döneminde Ebû'l-Kâsım Nîsâbûrî'nin Tahrîr usûl Uklîdis'i ve Harzemşâhlar döneminde Harakî çizgisindeki Şemseddin Çağmînî'nin yine bir tür tahrîr olan Kitâb Telhîs Uklîdis'i ile Esîrüddin Ebherî'nin Islâh Uklîdis'i bu durumu temsil eden en iyi örneklerdir.

Bu özellikleri haiz böyle bir ortamda ortaya çıkan tahrîr yöntemi, aynı zamanda, ilk defa dizgeli olarak, Matematik bilimlerinin medrese ders müfredatlarına girmesini ve bu amaçla yine ilk defa olarak muhtelif Matematik bilimlerde ders kitaplarının hazırlanmasını doğurdu. Bu sonucun ortaya çıkmasında, yukarıda işaret edildiği üzere Gazalî'nin Matematik bilimler için sağladığı entelektüel meşrûiyet ortamında Bahâuddin Harakî ve öğrencilerinin İbn Heysem'i takip ederek doğanın bilgisinde, mantıkî olanın yanında ta‘lîmî olanın da gerekliliği konusunda ısrar etmeleri önemli bir rol oynamıştır. Hca-Talebe merkezli ve son derece sıkı ıstılâhî bir dille yazılmış ders kitapları aynı zamanda ilmî hayatın zihnî bağımsızlığı için de bir garantiydi. Bu çerçevede ilk eserin kadîm dönemde Matematik - doğa ilişkisini en iyi temsil eden Astronomi sahasında yazılması denilenleri destekler mâhiyettedir. Nitekim bizzat Harâkî, Muntehâ'l-idrâk fî dirâyeti'l-eflâk adlı teknik açıdan gelişmiş eserini et-Tabsîra fî ilmi'l-hey'e adıyla ihtisâr ederek ders kitabı formatında hazırlamıştır; Şerefuddin Mesûʻdî'nin el-Kifâye fî ilmi'l-hey'e adlı çalışması da benzer özellikleri gösterir. Ancak Matematik bilimlerde medrese müfredatı için ders kitabı hazırlama konusunda en dikkate değer isim hiç şüphesiz Harzemşahlar döneminin önemli ismi Şemseddin Çağmînî'dir. Hisâb, Cebir, Hendese ve Astronomi sahalarında ders kitapları hazırlayan Çağmînî'nin İslam medeniyetinde en uzun süreli etkili ve daha sonraki eserlere rol-model olan eseri hiç şüphesiz el-Mulahhas fi ilmi'l-hey'eti'l-basîta'dır. Matematik bilimlerdeki ders kitapları ve bunların medreselerdeki ta‘limî bilgi külliyatının, dönemin, çağdaş deyişle 'bilimsel paradigması" haline gelmesini sağlamış, süreç içinde bu daire genişlemiş; doktriner felsefî yaklaşım ortadan kalkarak perspektif yaklaşıma geçilmiş; bu da bir kişinin aynı anda hemen tüm farklı alanlarda uzman olmasına imkân vermiştir. Bu durumun en güzel örneği Matematik bilimlerdir; ister Meşşâî ister mütekellim olsun her bilim adamı artık kendi dönemindeki Matematik bilimlerin tasvir ettiği, açıkladığı Evren resmini benimsemiştir. Bu gelişme, süreç içinde ilmî bilgideki farklı yaklaşımlar arasındaki parçalanmışlığı gidererek paradigmatik bir birliğin oluşmasını sağlamıştır.Bu özellikleri haiz böyle bir ortamda ortaya çıkan tahrîr yöntemi, aynı zamanda, ilk defa dizgeli olarak, Matematik bilimlerinin medrese ders müfredatlarına girmesini ve bu amaçla yine ilk defa olarak muhtelif Matematik bilimlerde ders kitaplarının hazırlanmasını doğurdu. Bu sonucun ortaya çıkmasında, yukarıda işaret edildiği üzere Gazalî'nin Matematik bilimler için sağladığı entelektüel meşrûiyet ortamında Bahâuddin Harakî ve öğrencilerinin İbn Heysem'i takip ederek doğanın bilgisinde, mantıkî olanın yanında ta‘lîmî olanın da gerekliliği konusunda ısrar etmeleri önemli bir rol oynamıştır. Hca-Talebe merkezli ve son derece sıkı ıstılâhî bir dille yazılmış ders kitapları aynı zamanda ilmî hayatın zihnî bağımsızlığı için de bir garantiydi. Bu çerçevede ilk eserin kadîm dönemde Matematik - doğa ilişkisini en iyi temsil eden Astronomi sahasında yazılması denilenleri destekler mâhiyettedir. Nitekim bizzat Harâkî, Muntehâ'l-idrâk fî dirâyeti'l-eflâk adlı teknik açıdan gelişmiş eserini et-Tabsîra fî ilmi'l-hey'e adıyla ihtisâr ederek ders kitabı formatında hazırlamıştır; Şerefuddin Mesûʻdî'nin el-Kifâye fî ilmi'l-hey'e adlı çalışması da benzer özellikleri gösterir. Ancak Matematik bilimlerde medrese müfredatı için ders kitabı hazırlama konusunda en dikkate değer isim hiç şüphesiz Harzemşahlar döneminin önemli ismi Şemseddin Çağmînî'dir. Hisâb, Cebir, Hendese ve Astronomi sahalarında ders kitapları hazırlayan Çağmînî'nin İslam medeniyetinde en uzun süreli etkili ve daha sonraki eserlere rol-model olan eseri hiç şüphesiz el-Mulahhas fi ilmi'l-hey'eti'l-basîta'dır. Matematik bilimlerdeki ders kitapları ve bunların medreselerdeki ta‘limî bilgi külliyatının, dönemin, çağdaş deyişle 'bilimsel paradigması" haline gelmesini sağlamış, süreç içinde bu daire genişlemiş; doktriner felsefî yaklaşım ortadan kalkarak perspektif yaklaşıma geçilmiş; bu da bir kişinin aynı anda hemen tüm farklı alanlarda uzman olmasına imkân vermiştir. Bu durumun en güzel örneği Matematik bilimlerdir; ister Meşşâî ister mütekellim olsun her bilim adamı artık kendi dönemindeki Matematik bilimlerin tasvir ettiği, açıkladığı Evren resmini benimsemiştir. Bu gelişme, süreç içinde ilmî bilgideki farklı yaklaşımlar arasındaki parçalanmışlığı gidererek paradigmatik bir birliğin oluşmasını sağlamıştır.

 

Matematik bilimler söz konusu olduğunda bu dönemde başlayan ve tahrîr döneminin en önemli karakteristiği haline gelen diğer bir husus Sultan Sencer'in etrafındaki bilginlerle başlayan, ancak Fahreddin Râzî ile felsefî bir içerik kazanan matematik nesnelerin ontolojisi ile doğaya ilişkin matematiksel bilginin meşrûiyeti konusundaki tartışmalar ve bu tartışmaların etrafında yürütüldüğü nefsu'l-emr kavramının icadıdır. Matematik bilimleri ile Matematik felsefesi ve Matematik - doğa ilişkisi açısından son derece önemli olan bu gelişme daha sonraki yüzyılların en önemli konularından biri olmaya devam edecektir. Yine aynı dönemde Fahreddin Râzî'nin çağdaşı Şehâbeddin Sühreverdî geliştirdiği İşrâkî felsefede maddî doğanın asgarî ontik birimini mikdâr(imtidâd, extentio) kabul etmiş; bu da Doğa'nın hendesî-hisâbî idrâki için bir kapı aralamıştır. Tahrîr döneminde pek çok matematikçi filozofun İşrâkî meşrep olmasının, İşrâkî felsefenin söz konusu ontolojik kabulüyle sıkı bir ilişkisi vardır. Ayrıca İbn Fellûs örneğinde olduğu üzere, bahusus Hanefî fakihlerinin matematik bilimlerin Kitâb-i Tenzîlî'nin emir ve nehiylerini anlama ve uygulamada işe yarar olduğunu görmeleri, Kitâb-i Tekvînî'de de benzer durumun söz konusu olabileceği inancını beslemiş olmalıdır; nitekim bu yaklaşım tahrîr döneminde Şâfîʻî fakihleri tarafından da benimsenecektir.

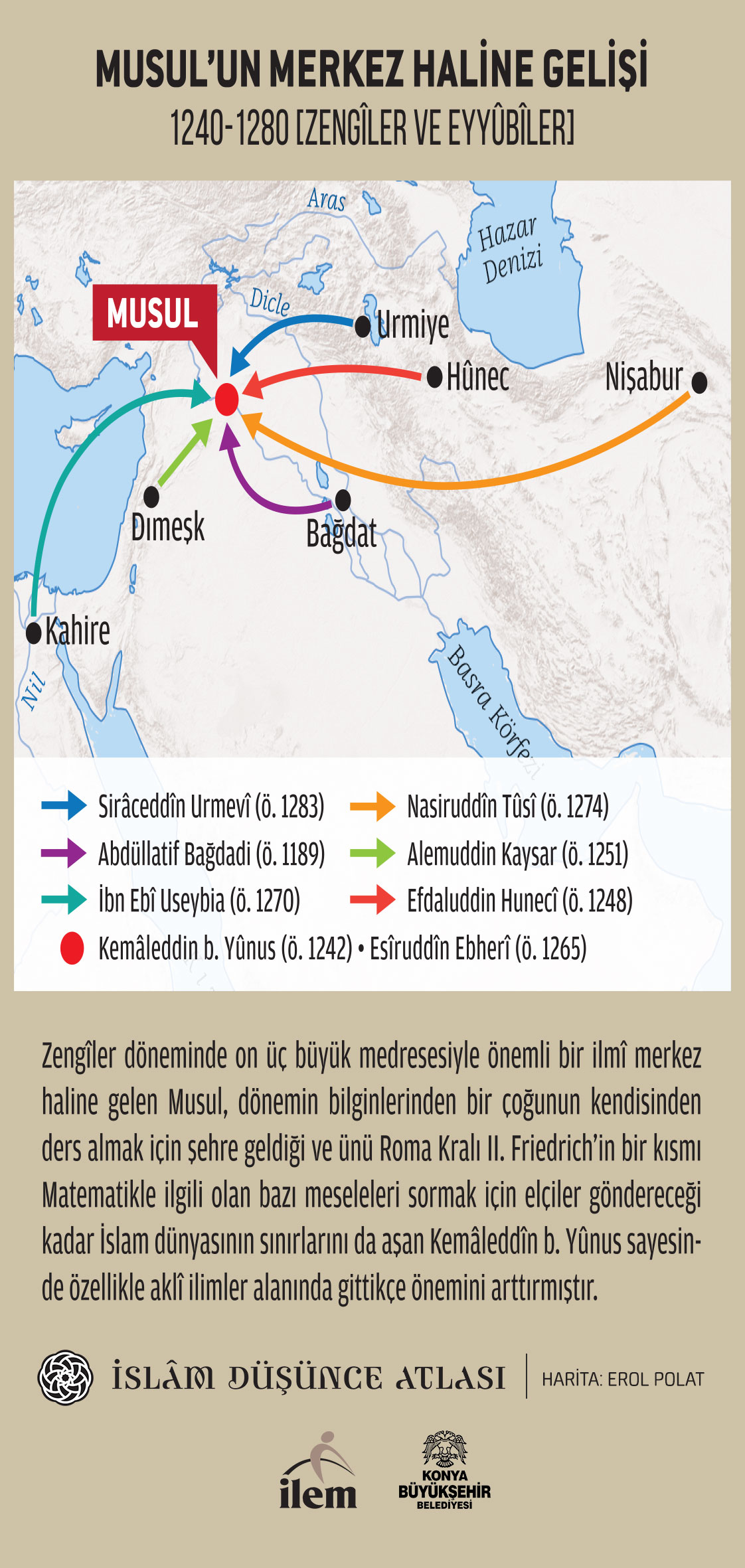Şimdiye değin fırça darbeleriyle özetlenen bu durum, yukarıda da işaret edildiği üzere, Sultan Sencer'in önce siyaseten zayıflaması, akabinde de ölümüyle istikrarını kaybetti ve ileri gelen bilginler daha Doğu'ya doğru yola çıktılar; Moğol istilası ile bu yola çıkışlar hem hızlandı hem de yola çıkanların sayısında ciddi bir artış oldu. Bu bilginler hem kendi bilgi ve görgülerini yeni coğrafyadaki meslektaşlarına aktardılar hem de kendileri bu coğrafyalardaki birikim ile ilişki kurdular. Bu duruma en iyi örneklerden biri, Esîrüddin Ebherî'nin Türkistân'dan, Nasirüddin Tûsî'nin İran'dan, Alemüddin Kaysar'ın Mısır'dan gelerek ders halkasına dahil oldukları ve ileri seviyedeki matematik bilimleri tahsil ettikleri Kemâleddin b. Yunus'un Musul'daki medresesidir. Bu medrese hem bir tür akademi hâline gelerek yetişmiş bilginlerin dönemin en önemli matematikçi filozofu elinde yüksek matematik bilimleri tahsil etmesini sağladı hem de sahip oldukları farklı arka-planlarını kendi aralarında paylaşmalarına imkân verdi.

Merv'in dönüşen ve zenginleşen bir devamı olarak gördüğümüz matematik bilimlerdeki tahrîr dönemi, sekiz coğrafî merkez etrafında incelenebilir. Birincisi tahrîr hareketine kurumsal bir kimlik kazandıran ve kendinden sonraki merkezleri besleyen Merağa matematik-astronomi okulu ile bu okulun, kendine has özelliklerine rağmen, doğrudan bir devamı olan Tebrîz Şenb-i Gâzân matematik-astronomi okulu; bu okulun beslediği ancak kendi mahallî birikimlerinin de önemli olduğu Endülüs-Mağrib ile Şâm-Kâhire kültür havzaları ve Merv ile Merâğâ'nın doğrudan mirasçısı, kelâmî vurgunun baskın olduğu Timûrîler dönemi Semerkand matematik-astronomi okulu; matematik bilimler açısından doğrudan Tebrîz'in donattığı Saray merkezli Altın-Orda ve Hind-Babür coğrafyası ile daha önce Merağa ve Tebrîz'in arka-planını oluşturduğu, kendinin de hem beslediği hem de beslendiği Semerkand'ın birikimini büyük oranda tevârüs eden Bursa-İstanbul. İslam medeniyetindeki bu merkezler yanında Merağa'nın kısmî olarak etkilediği Moğol Yuanlar dönemi Çin'i ve Gregory Choniades üzerinden Tebrîz'in olağanüstü etkisinde kalan Trabzon İmparatorluğu ile İstanbul Bizans İmparatorluğu bu merkezlere ilave edilebilir.

Moğolların, büyük bir yıkım eşliğinde Dünya'nın %22’sini ele geçirerek kurdukları bitişik sınırlı 30 milyon lik büyük kara imparatorluğu en genel anlamıyla Doğu ile Batı ve Kuzey ile Güney'i birleştirmiş; bir Pax Mongolica yaratmıştı. Yıkımın hemen akabinde İslâm coğrafyasında yavaş da olsa yeniden bir inşa süreci başlamış; özellikle Moğol posta teşkilatı olan Ham sistemi sayesinde sadece asker ve resmî evrak değil, para, bilgi, kitap, bilgin vb. eşya ve insan dolaşımı için güvenli bir ortam oluşmuştu. Bu ortam içinde Nasirüddin Tûsî, İlhanlı hükümdarı Hülâgu'nun hükmettikleri coğrafyadaki vakıflara ait gelirlerin %10unu tahsis ederek desteklemesiyle Merağa matematik-astronomi okulunu kurdu; rasathane yanında kütüphane, medreseler, âlet üretim atölyeleri gibi büyük bir külliyeyi inşa etti; binlerce kitabı topladı ve döneminin Mueyyeddin Urdî, Muhyiddin Mağribî, Necmeddin Kâtibî, Kutbuddin Şîrâzî gibi en önemli matematik-astronomi bilginlerini davet etti. Bu süreç sonucunda tahrîr hareketine kurumsal bir kimlik kazandırıldı, yeni araştırmalar yapıldı, eserler telif edildi, öğrenciler yetiştirildi.

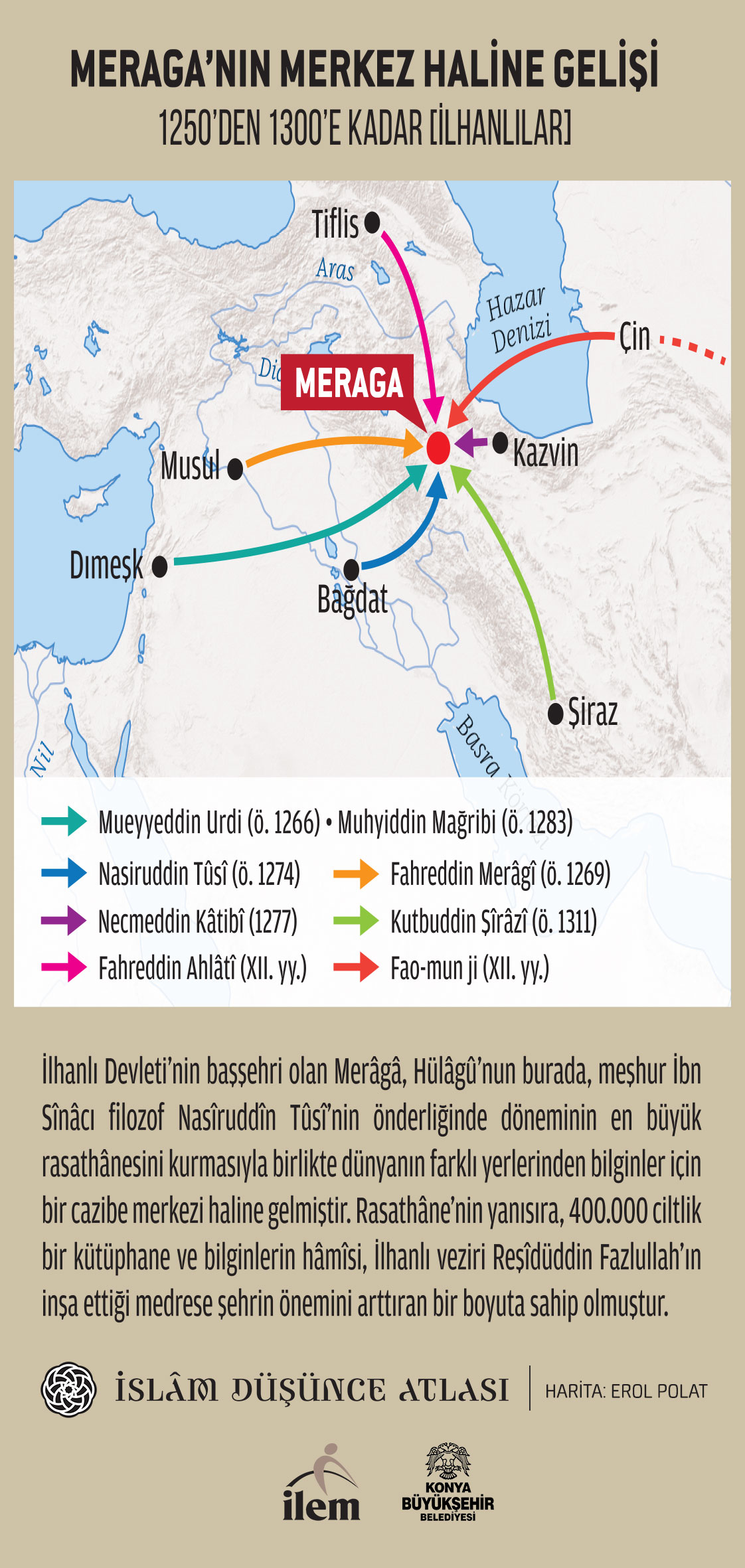
Okulunun kurucu ismi Nasirüddin Tûsî her ne kadar saf bir İbn Sinacı filozof olarak görülse de Merağa'nın kendine konu kıldığı şey daha çok İbn Heysem'in Şukûk'undaki temel tezlerdi. Ayrıca doğa ile matematik birlikteliği benimsendi ve çalışmalar daha çok "gözlem ile uyumlu hesap/model" ilkesi üzerinden yürütüldü. Bu çerçevede Tûsî, Taşköprülü-zâde'nin 'yeni bir yazım yöntemi' icadı olarak gördüğü, Merağa'dan önce 1247'de Tahrîru'l-Macestî, 1248'de Tahrîr usûli'l-hendese ve'l-hisâb adlı iki önemli eserle ilk ürünlerini verdiği tahrîr projesine, kurumsal bir kimlik kazandırarak neredeyse ömrünün sonuna kadar sürdürdü ve Helenistik ve klasik İslâmî dönemlerde kaleme alınmış matematik bilimlere ilişkin yirmi temel metni tahrîr etti. Merağa'daki tahrîr faaliyeti yalnızca Tûsî'ninkiyle sınırlı değildi; okulun Endülüs-Mağrib'ten gelen önemli üyesi Muhyiddin Mağribî, bir kaç küçük eser dışında, Hâzin, İbn Sînâ ve Ömer Hayyâm'ın konuyla ilgili görüşlerini de dikkate alarak Usûlu'l-hendese'yi de tahrir etmişti. Diğer bir teşebbüs Tûsî'nin öğrencisi Kutbuddin Şîrâzî'ye aittir. Şîrâzî, Durretu't-tâc ve gurratu'd-dibâc adlı Farsça bilimler ansiklopedisi çalışmasında Usûlu'l-hendese'yi Farsça'ya çevirirken tahrîr de etti. Tûsî'nin oğlu Sadreddin Alî'ye nispet edilen ve 1594'de Roma'da basılan, başta beşinci postulat sorunu olmak üzere hendese ile ilgili Tûsî'nin son dönem düşüncelerini içeren Tahrîru ısûli'l-hendese de önemli bir çalışma olarak kabul edilebilir. Son olarak önemli bir teşebbüs Merağa'nın üçüncü müdürü ve Tûsî'nin oğlu Asîluddin Hasan zamanında İbn Sertâk'ın, Endülüs-Mağrib geleneğini temsil eden Mu'temen b. Hûd'un hendesî matematiğe ait önemli eseri el-İstikmâl fî ilmi'l-hendese'yi el-İkmâlu'l-Asîlî fî'l-hendese adıyla tahrîr etmesidir.

Şimdiye değin sıkça kullanılan tahrîr ne demektir? Matematik bilimler söz konusu olduğunda tahrîr: 1. Metnin hem dil hem de teknik içerik anlamında müstensih hatalarından temizlenmiş sahîh bir nüshasını elde etmek; 2. Metnin yazımından itibaren tarihî süreçte, ister nazarîye ister yeni değerler olsun, konunun teknik içeriğiyle ilgili ortaya çıkmış önemli gelişmeleri metne dahil ederek metni güncellemek; 3. Mevcut ispatları gözden geçirerek daha dakik hale getirmek; yeni ispatlar vermek; var ise ispatsız nazarîyeleri -mümkünse- ispatlamak; 4. Nazarîyeleri, yeni gelişmeler ışığında, gerekiyorsa, bölmek, birleştirmek, kısaltmak vb. işlemlere tâbi tutmak; 5. Metnin nazarîye - ispat tertibini gözden geçirmek; gerekiyorsa takdîm-te'hîr etmek; 6. Istılâh birliği sağlamak; 7. Nihâyet tüm bu işlemlerden sonra metni iç-tutarlılık açısından gözden geçirmek. Bir metin için tüm bu işlemler yapılacağı gibi, şartlara göre biri veya bir kaçı da tercih edilebilirdi. Bu işlemlerde dikkat edilmesi gereken en önemli nokta, tahkîk yönteminde olduğu gibi, matematik bilimlerde tartışmalı tüm deliller zikredilmez; ulaşılan ve en doğru olduğu kabul edilen delil verilmekle yetinilir. Öte yandan bu dönemde tahrîr yanında her biri ayrı bir yazım tekniği olan ve farklı anlamlara gelen, tenkîh, tehzîb, tecrîd, telhîs, ihtisâr, mulahhas, muhtasar, muhassal, mahsûl, metâlib ve elbette şerh, hâşiye ve ta‘lîk gibi yöntemler de mevcuttu. En genel anlamıyla tahrîr okuması bir tür bilginin tarihselleştirilmesi anlamına gelir; gerçekten de hem tahkîk hem de tahrîr yöntemi İslam medeniyetinde tarihsel epistemolojinin bir türü olarak okunabilir.

***

Şimdiye değin genel çerçevesi verilen tahrîr dönemindeki kültür havzalarını dikkate alarak matematik bilimlerin gelişmeleri ana hatlarıyla şöyle özetlenebilir: Sittînî hesap genel hesap kitapları içinde ve hazırlanan zîclerin girişlerinde ele alınmaya devam etti. Ancak bu dönemde özellikle Kâhire-Şâm kültür havzasında pratik astronomi, astronomi âletleri ve yeni bir ilim dalı olarak kurulan ilm-i mîkât'ın gereksinimleri doğrultusunda İbn Mecdî Keşfu'l-hakâik fî hisâbi'd-derec ve'd-dekâik adıyla bağımsız bir risale kaleme aldı; öğrencisi Sıbt Mardînî tarafından Rekâiku'l-hakâik fî hisâbi'd-derec ve'd-dekâik adıyla şerh edilen eser, tüm İslam coğrafyasında temel başvuru metni oldu; üzerine başta Sıbt Mardînî'nin kendi olmak üzere pek çok matematikçi-astronom tarafından muhtelif içerikte onlarca çalışma yapıldı.

Zihin hesabı alanında tahrîr dönemindeki en önemli gelişme, bazı yeni işlem tekniklerinin yanında, bu hesap dizgesinin ispatlı bir biçimde kuruluşudur. Tûsî'nin öğrencisi İbn Havvâm, Bağdâd'da el-Fevâidul'-behâiyye fî'l-kavâidi'l-hisâbiyye adlı bir eser telif etti; öğrencisi ve eseri bizzât kendinden okuyan Tebrîz Şenb-i Gazan matematik-astronomi okulunun önemli temsilcisi Kemâleddin Fârisî hocasının eserini Esâsu'l-kavâid fî usûli'l-fevâid adıyla üst seviyede şerh ederek, eserde verilen hemen tüm kuralları sıkı bir hendesî ispat sürecine tabi tuttu (isbât bi'l-hutût); böylece zihin hesabı ispatlı bir biçimde bir bilim olarak yeniden kuruldu. İbn Havvâm'ın diğer bir öğrencisi İmâdudin Kâşî, hocasının eserine İzâhu'l-mekâsıd li'l-ferâidi'l-fevâid adıyla yeni bir şerh yazdı ve verilen kuralları adedî yöntemle ispat etti. Bu eserler Balkanlar - İstanbul -Anadolu - Kuzey Suriye - Irak - İran ve Türkistân coğrafyasında belirli bir müddet ders kitabı olarak okutuldu; o kadar ki, XVII. yüzyılda bile Katip Çelebî, zihin hesabını en iyi temsil eden eser olarak Fevâid'i görmekteydi. Zihin hesabı alanında günlük hayata taalluk etmesi, insan bedeni dışında yazı malzemesine ihtiyaç duymaması ve oldukça basit ve hızlı hesap kurallarını muhtevi olması nedeniyle Kâhire-Şâm hattında çokça eser kaleme alınmıştır. Bu sahada özellikle İbn Hâim'in çalışmaları, bahusus zihnî hesap konusunda bir tür ansiklopedi olan el-Maûne fî hisâbi'l-hevâî adlı eseri zikredilebilir; ayrıca bu eser üzerine başta müellifi olmak üzere pek çok matematikçi tarafından çalışmalar yapılmıştır. Yine Kâhire-Şâm kültür havzasında yetişmiş matematikçi Sıbt Mardinî'nin Tuhfetu'l-ehbâb fî ilmi'l-hisâb'ı en yaygın kullanılan ders ve başvuru metinlerinden biri olmuştur. Bu alanda İstanbul'da meçhûl bir müellif tarafından kaleme alına İrşâdu't-tullâb ilâ ilmi'l-hisâb adlı eser konuyla ilgili hemen tüm kuralların dökümünü verir ve bazı kuralları da adedî olarak açıklar. Bu hesap hakkında tahrîr döneminde onlarca eser yazılmasına karşın, XVI. yüzyılın sonuna doğru başta kağıt olmak üzere yazı malzemelerinin yaygınlaşması; okuma-yazma bilen tahsilli orta-sınıfın çoğalması vb. nedenlerle yavaş yavaş ortadan kalmış ve hind hesabı içinde erimiş, varlığını pratik kurallar manzûmesi olarak sürdürmüştür.

Hind hesabı tahrîr döneminin hem nicelik hem de nitelikçe en çok eser verilen dönemdir; denebilir ki, Harizmî tarafından kurulan ondalık-konumlu algoritmik hesap tekniği bu dönemde kemâle ermiştir. Hesap sahasında yapılan tüm özgün keşifler de bu hesap dizgesi içinde vukû bulmuş; özellikle ondalık kesirler bu dizge içinde varlığa gelmiştir. Merağa'dan Nasirüddin Tûsî'nin Cevâmiu'l-hisâb bi't-taht ve't-turâb'ı; Tebrîz'den Cemâleddîn Türkistânî'nin, bir süre ders kitabı olarak da kullanılan er-Risâletu'l-Alâiyye fî'l-mesâili'l-hisâbiyye'si; bu esere Alî Garbî'nin yazdığı hacimli ve XIV. yüzyıl matematiğinin adeta bir dökümü olarak görülebilecek el-Muʻcizâtu'n-Necîbiyye fi şerhi'r-risâleti'l-Alâiyye adlı şerhi; yine Tebrîz'e mensup Kutbuddin Şîrâzî'nin talebesi Şemseddin Nîsâbûrî'nin Anadolu - İran hattında ders kitabı olarak da kullanılan eş-Şemsiyye fî'l-hisâb'ı ilk elde dikkati çeken eserlerdir. Tebrîz havzasının bu alandaki diğer önemli bir katkısı da ilk ve tek olarak İmâduddin Kâşî'nin Lubâbu'l-hisâb adlı eserinde 'el-hisâbu'l-hevâî' adını verdiği zihin hesabı ile hind hesabı arasında dizgeli bir mukayese yapmasıdır.

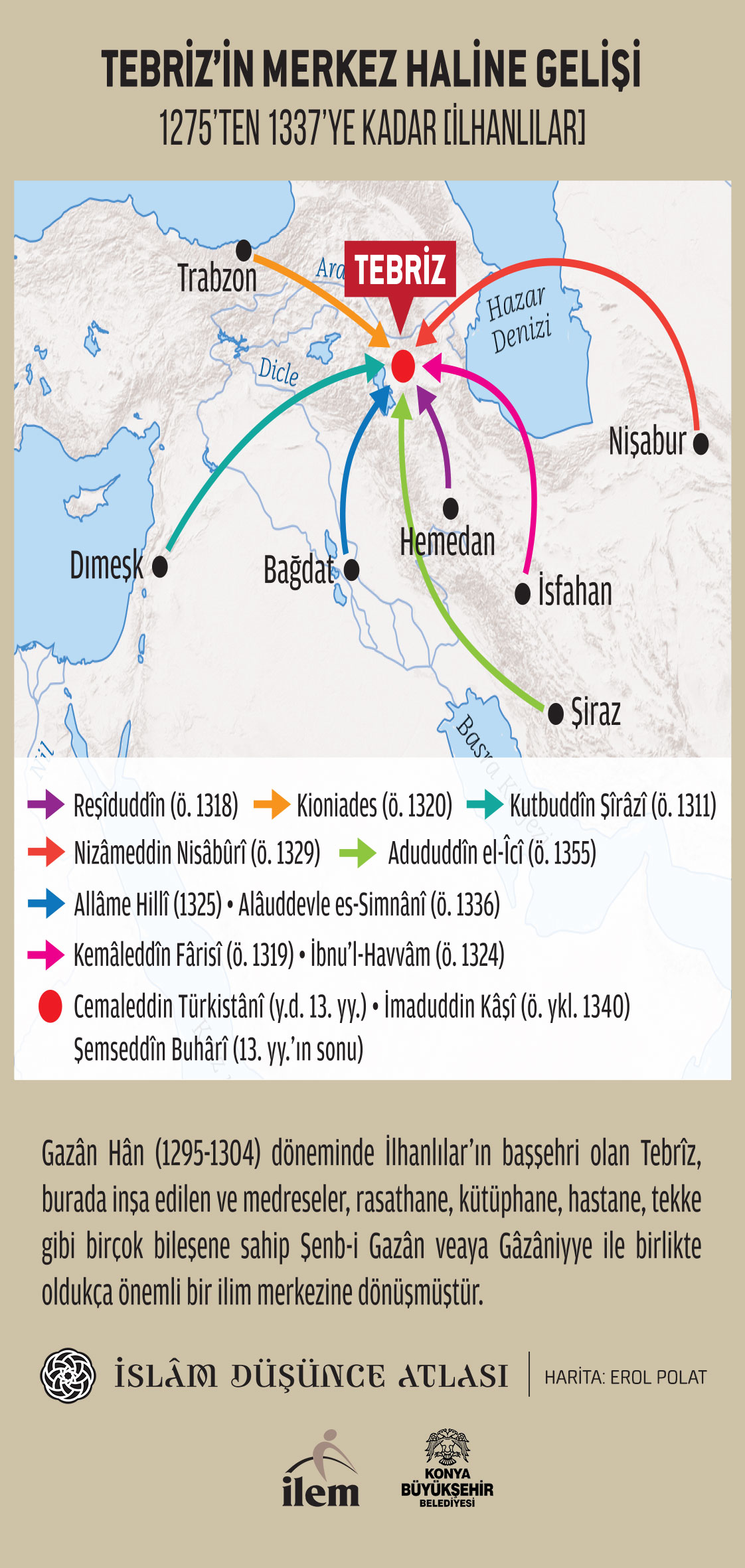Bu dönemde Merağa ve Tebriz'den beslenen Mağrib kültür havzası, hind hesabında ciddi bir atılım gösterir ve İbn Bennâ ile ilk gerçek Matematik geleneğini kurar. İbn Bennâ'nın el-Makalât fî ilmi'l-hisâb adlı çalışması yanında Telhîs amâli'l-hisâb adlı eseri tarihte yaygın ve sürekli gelenek oluşturan nadir eserlerden biridir ki, başta müellifin kendisi buradaki fikirlerini savunmak için Keşfu'l-hicâb an vucûhi aʻmâli'l-hisâb adlı bir kitap kaleme almış; Mağrib okuluna mensup İbn Kunfûz, İbn Haydûr ve İbn Merzûk gibi pek çok matematikçi tarafından da şerh edilmiştir. Telhîs teknik içeriği yanında, Matematiğin ilkeleri, sayının tanımı ve sonsuzluk kavramı hakkındaki mülahazaları ile de dikkat çekmiştir. Mağrib okulunun Matematik bilimlerde son büyük temsilcilerinden biri, diğer pek çok eseri yanında Keşfu'l-esrâr an ilm hurûfi'l-gubâr adı kitabıyla tanınan Kalasâdî'dir. Yine aynı bölgeye mensup İbn Gâzî'nin etkili olmuş Buğyetu'l-tullâb fî şerh munyeti'l-hisâb adlı eseri de dikkat çekmektedir.

Mağrib havzasındaki bu gelişmeler, kendine en yakın coğrafya olan Kâhire - Şâm hattını etkiledi ve İbn Bennâ'nın eserleri dikkate alınmaya başlandı. Bu eserin gelişmiş algoritmik düzeyi, İbn Haldûn'un şikayet etiği hacmi küçük muhtevası yoğun yapısı, muhtevi olduğu teknik bilgi ve felsefî-nazarî iddiaları özel bir dikkat çekti. Aynı zamanda Kâhire - Şâm havzasının pratik yönelimi de bu ilgiyi besledi. Zihin hesabında olduğu gibi, bu alanda da daha sonra yaygın olarak kullanılan pek çok eser yazan İbn Hâim, İbn Bennâ'nın eserlerine özel bir ilgi göstermiştir. Ancak Telhîs üzerine en önemli, hacimli, özgün ve etkili çalışmayı İbn Mecdî, Hâvî'l-lubâb fî şerh telhîs amâli'l-hisâb adıyla yapmıştır. Mağrib, Kâhire-Şâm havzasının hind hesabı içindeki en önemli başarılarından biri, İbn Mecdî ve İbn Gâzî'nin eserlerinde olduğu gibi hem genel hesap kitapları içinde, hem de İbn Ebî'l-Feth es-Sûfî'nin İrşâdu'l-ʻacem li-aʻmâli cuzûri'l-esamm adlı bağımsız çalışmasında olduğu gibi özellikle irrasyonel sayılar aritmetiği konusunu ayrıntılı bir biçimde incelemesidir. İlginçtir ki, bu dönemde Özbek Hânlığı yönetiminde Altın-Orda Devleti'nde, Kırım'da hind hesabı ile ilgili, Muhammed Kâsânî tarafından yazılan et-Tuhfe fî ilmi'l-hisâb yalnızca teknik içeriği ile değil aynı zamanda verdiği tarihi bilgilerle de önemlidir. Bu eser aynı zamanda Altın-Orda Devleti'nin Özbek Hanlığı zamanında ilmî açıdan da Dâru'l-İslâm'ın bir parçası olmaya başladığını gösterir.

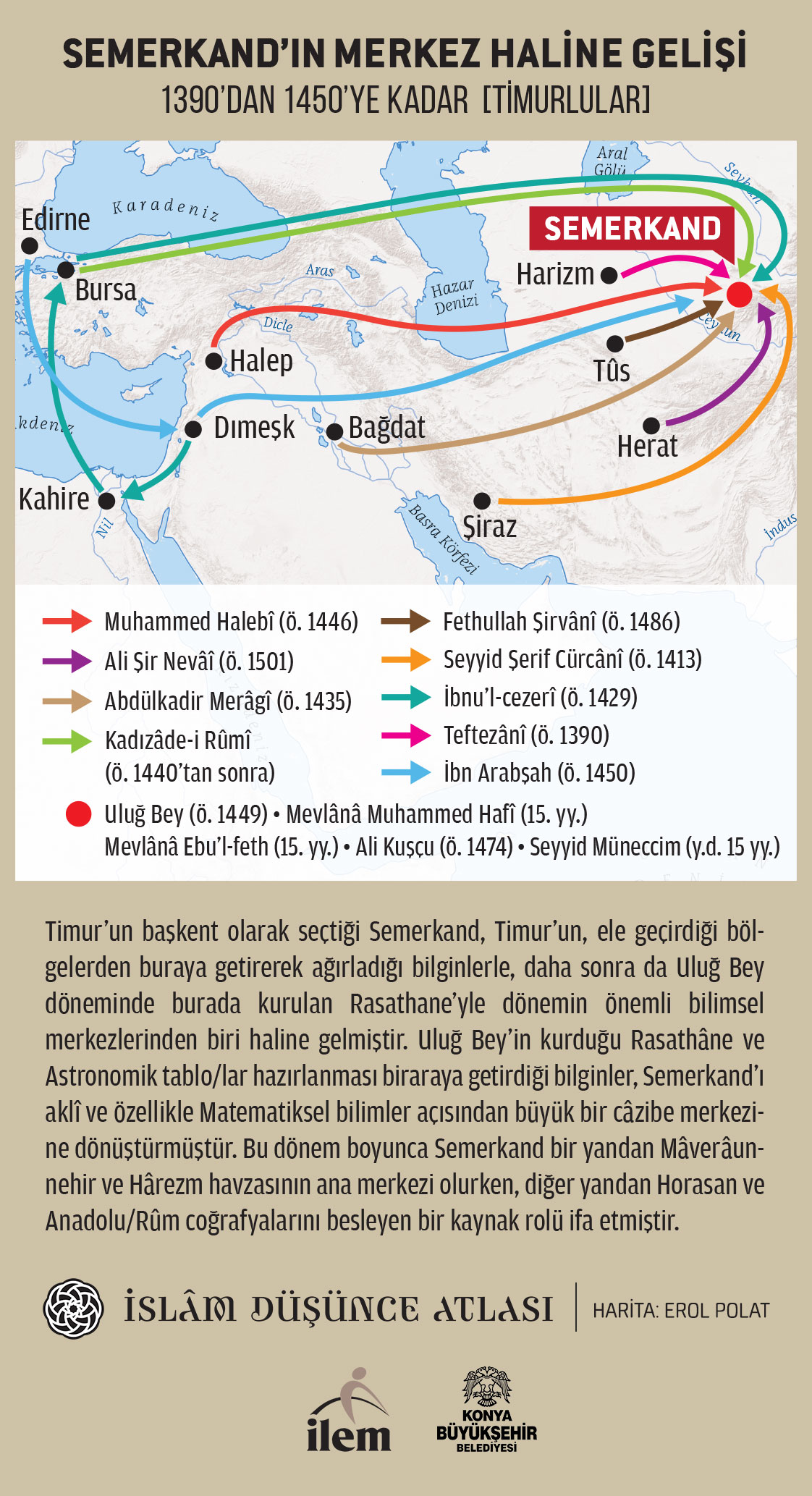Hind hesabı alanında önemli eserlerin verildiği diğer bir yer Semerkand Matematik-Astronomi okuludur. Semerkand Rasathanesi'nin ilk müdürü matematikçi-astronom Cemşîd el-Kâşî, Miftâhu'l-hussâb adlı eserinde konuyla ilgili tüm tarihî birikimi dizgeli bir biçimde ele almakla kalmamış, aynı zamanda ilk defa olarak ondalık kesirler aritmetiğini dört temel işlem düzeyinde ifade etmiştir. Öte yandan eser, daha önce Tebrîz'de Cemâleddîn el-Türkistânî'nin Arap dil bilim geleneğinden hareketle öne sürdüğü ve şârihi Alî el-Garbî'nin oldukça ayrıntılı bir biçimde tartıştığı sayı tanımını merkeze almıştır. Semerkand okulu mensubu Ali Kuşçu, İstanbul'a havzasına geldiğinde hem Miftâh'ı hem de Fevâid'i birlikte göz önünde bulundurarak er-Risâletu'l-Muhammediyye fî'l-hisâb adıyla özetlemiş, sayı tanımını olduğu gibi benimsemiş, bu eser bir müddet ders kitabı olarak kullanılmıştır.

İstanbul havzasında hind hesabı alanında en önemli katkılar şöyle özetlenebilir: Mevcut eserlerin korunması, istinsah yoluyla çoğaltılması yanında, başta kağıt olmak üzere yazı malzemelerinin kısmî bolluğu nedeniyle hem devlet dairelerinde kullanılmış hem de medreselerde öğretilmiştir; bu da onun resmî hesap dizgesi olarak kabul edilmesini sağlamış ve toplumsallaştırmıştır. Özellikle devlet muhâsebe kalemlerinde çalışan muhâsib ve kâtibler için ortaya uygulama karakteri ağır basan bir hind hesabı türü çıkmış ve bunun için, Mehmed Atmaca'dan, Kâtib Alâaddin Yusûf, Yusûf Bursevî ve Matrakçı Nasuh'a kadar büyük çoğunluğu Türkçe olan muhâsebe matematik metinleri telif edilmiştir. Bu metinler hem pratik problemler bakımından hem de ondalık kesirlerin kullanımı açısından son derece önemlidirler. Ancak bunun yanında İstanbul Rasadhânesi'nin kurucusu Takiyeddin Râsıd, Buğyetu't-tullâb fî ilmi'l-hisâb adlı eserinde ondalık kesirler aritmetiğini, Cemşîd el-Kâşi'nin bıraktığı yerden sürdürerek geliştirmiştir. Hind hesabı söz konusu olduğunda tahrîr dönemindeki en son ve en önemli metin, XVI. yüzyılın Türkçe telif etmek karakterine uygun olarak yazılan, İbn Hamza'nın 1599'da kaleme alıp Sultan III. Murad'a sunduğu Tuhfetu'l-aʻdâd li-zevî'r-ruşd ve's-sedâd adlı Batı Türkçesiyle telif edilmiş eserdir. Eser hind matematiği ile ilgili birinci bölümünde konuyla ilgili tüm tarihsel birikimi bir araya getirmiş; özellikle Endülüs - Mağrib ve Kâhire havzalarının birikimini ayrıntılı olarak yeniden ifade etmiştir. Matematik bilimlerdeki bu entegrasyon yalnızca Anadolu - Şâm -Kâhire ve Mağrib bölgelerinde görülmez; XVI. yüzyılın er-Risâletu'l-nâfiaʻ fî'l-hisâb ve'l-cebr ve'l-misâha adlı önemli ve hacimli matematik kitabını kaleme alan Hindistan kökenli Abdulmecîd Sâmûlî de eserinde İslam coğrafyasındaki tüm önemli eser ve isimleri kullanır. Bu durum, Osmanlı Devleti'nin hem maddî hem de manevî anlamda Dâru'l-İslâm kavramını tekrar ihyâ ettiğini gösterir.

İslam medeniyetinin klasik çağında Cebir, Harizmî'den Şerefuddin Tûsî'ye değin hem çok terimliler hesabı hem de birinci ve ikinci derece denklemlerin adedî ve hendesî çözümü konusunda zirveye ulaşmıştı. Lafzî olması, pozitif köklerin tespit ile yetinmesi ve çözüm teknikleri ile doğal sınırlarına ulaşan Cebir tahrîr döneminde daha çok içe doğru derinleşmiştir. Hem Şerefuddin Tûsî'nin çalışması hem de Esîruddîn Ebherî'nin eseri kayıp olmakla birlikte, bunların varlığı bile tahrîr döneminin hemen öncesinde Merv kökenli bir cebir geleneğinin Anadolu'ya ve orta-İslam dünyasına geldiğini gösterir. Tebrîz'de Kemâleddin Fârisî'nin Esâs'ta ispatlı bir biçimde incelediği çok terimliler aritmetiği ile denklem analizleri; Cemşîd el-Kâşî'nin Miftâh'daki gayretleriyle belirli bir olgunluğa erişmiştir. Kâşî, ayrıca dördüncü derece denklemleri de ele alan bir eser yazmakla birlikte bu eser zamanımıza ulaşmamıştır, ancak bu bilgi bize Ebherî'den sonra da yüksek dereceli denklemlerle uğraşıldığını ve Semerkand'da dizgeli olarak incelendiklerini gösterir. Bu alanda Mağrib havzasının katkısı, İbn Bedr, İbn Bennâ, Kalasâdî ve İbn Gâzî gibi bilginlerinin eserlerinin gösterdiği gibi teknik anlamda ikinci dereceli denklemlerle sınırlı olsa da, İbn Kunfuz'dan itibaren cebirsel notasyon ve sembollerin keşfi ve yaygın olarak kullanılması; bu keşfin önce Kâhire'ye ulaşması ve İbn Mecdî gibi matematikçiler tarafından dikkate alınması önemlidir. Söz konusu keşfe tahrîr döneminde Mağrib ve Kâhire tecrübesini de dikkate alarak en son şeklini İbn Hamza Tuhfe'de vermiştir. Cebir söz konusu olduğunda Kâhire okulunda dikkat edilmesi gereken diğer önemli bir isim İbn Hâim'dir; yalnızca bu alanda yazdığı ders kitapları değil, el-Mumtiʻ fi şerhil-muknîʻ adlı eserinde İslam cebir geleneğindeki pek çok sorunu ele aldı; hendesî cebir yaklaşımını şiddetle eleştirdi; ikinci dereceden yüksek denklemlerin adedî olarak çözülebileceğini örneklerle gösterdi; ayrıca tespit edilebildiği kadarıyla ilk defa olarak tarihte 'menfî'(negatif) ve 'musbet'(pozitif) kavramlarını icat etti. Ali Kuşçu da İstanbul'da telif ettiği Muhammediyye'de bu kavramları -belki de İbn Hâim’den bağımsız olarak- kullandı. Öte yandan Sultan II. Bâyezid'e sunulan İrşâd'da meçhul bir müellif yüksek dereceli denklemler için genel çözüm arayışına girişti. Özellikle XV. ve XVI. yüzyıllardaki çok terimliler aritmetiği ve ikinci derece denklemler cebri konusundaki birikimi, Abdulmecîd Sâmûlî, er-Risâletu'l-nâfia fî'l-hisâb ve'l-cebr ve'l-misâha adlı önemli ve hacimli matematik eserinde dizgeli ve oldukça ayrıntılı bir biçimde inceler. Cebir söz konusu olduğundan Semerkand ve İstanbul'da vukû bulan önemli bir gelişme de, bazı trigonometrik fonksiyonların cebirsel analizidir; Cemşîd el-Kâşi, Musa Kadı-zâde, Ali Kuşçu, Mirim Çelebi ve Takiyeddin Râsıd bu duruma örnek verilebilir.

Hendese söz konusu olduğunda hiç şüphesiz söylenecek ilk söz hemen tüm hendesî matematiğe ait eserlerin, yukarıda da ayrıntılı anlatıldığı üzere Merv, Merağa, Tebrîz ve Tokat'ta tahrîr edildiğidir. Özellikle Nasirüddin Tûsî, Muhyiddin Mağribî, Kutbuddin Şîrâzî ve İbn Sertâk'ın çalışmaları bu faaliyetin en yüksek örnekleri olarak görülebilirler. Merağa'daki hendese çalışmaları yalnızca tahrirlerle sınırlı değildir; Hüsâmeddin Sâlâr, Muhyiddin Mağribî, Kutbuddin Şîrâzî gibi isimler paraleller postulatı ile ilgili metinler üretmiş; bahusus Tûsî kendinden önceki tüm birikimi dikkate alarak, konuyla ilgili tarihteki ilk bağımsız metni er-Risâletu'ş-şâfiye ani'ş-şekk fî'l-hutûti'l-mutevâziye adıyla telif etmiş; bu konuda Alemüddin Kaysar ile mektuplaşmıştır. Semerkand ve İstanbul hattında ise hendese alanında Musa Kadı-zâde, Ebû İshak Kirmânî ve Kehhâl Musa gibi bilginler eserler kaleme almıştır. Tebrîz'de ise Kemâleddin Fârisî ilginç bir çalışmaya imza atar; kendinden önceki, özellikle İbn Sînâ ve İbn Heysem'in düşüncelerini dikkate alarak modern öncesi dönemde açı(zâviye) hakkında en önemli ve hacimli kitabı kaleme alır: Risâle fî'z-zâviye. Fârisî eserinde kadîm matematikteki tüm açı türlerini ve hendesî değerlerini inceler.

Tahrîr edilen hendese eserleri arasında koni kesitleri ile ilgili Apollonius'un Kutûuʻ'l-mahrûtât'ı, Sabit b. Kurre ve diğer bilginlerin konuyla ilgili eserleri mevcuttu. Öte yandan Kutbuddin Şîrâzî, Tebrîz'de Kutûuʻ'l-mahrûtât'ı telhîs etti; İbn Sertâk, Tokat'ta el-İkmâl adıyla tahrîr ettiği İbn Hûd'un el-İstikmâl adlı eserinde koni kesitlerini saf hendese açısından ayrıntılı bir şekilde inceledi. Koni kesitleri alanında en yoğun incelemeler Semerkand matematik-astronomi okulunda yapıldı ve bu çalışmalar daha sonra İstanbul'a aktarıldı. Aburrezzâk Kâşânî, Ali Kuşçu, Fethullah Şîrvânî, Abdulalî Bircendî gibi bilginlerin eserleri yanında Kehhâl Musa'nın konuyla ilgili çalışmaları daha sonraki dönemleri de besledi. Saf hendese eserleri yanında koni kesitleri Fârisî'nin Esâs'ı, Kâşî'nin Miftâh'ı ve İbn Hamza'nın Tuhfe'si gibi büyük ölçekli hesap kitaplarında da Misâha(uygulamalı geometri) açısından ele alınmaya devam etti.

Trigonometri hemen tüm Astronomi hesaplarında kullanıldığından Merağa, Tebriz, Semerkand ve İstanbul Rasathaneleri'nde üretilen eserlerde mevcuttu. Ancak tahrîr döneminde Trigonometrideki en önemli gelişme, Nasirüddin Tûsî'nin tüm birikimi de değerlendirdiği Kitâb şekli'l-kattâʻ adlı çalışmasıyla bağımsız bir bilim dalı olarak kurulmasıdır; benzer bir çalışmaya çağdaşı Hüsâmeddin Sâlâr da teşebbüs etmiştir. Bu alandaki diğer bir gelişme, yukarıda da işaret edildiği gibi, trigonometrideki bazı denklemlerin, Kâşî, Kadı-zâde, Mirim Çelebî ve Takiyeddin'de görüldüğü üzere, Semerkand ve İstanbul havzalarında cebir yoluyla çözülmesidir. Trigonometri söz konusu olduğunda vurgulanması gereken başka bir gelişme de, İstanbul'da Takiyeddin Râsıd'ın tarihte ilk defa, sittînî(altmışlı) dizge ile hesaplanan trigonometrik fonksiyonların değerlerini ondalık kesirlerle tespit etmesidir.

Misâha yani uygulamalı hendese hemen tüm büyük-ölçekli hesap kitaplarının bir parçası olmaya devam etti. Ancak bu dönemde Misâha söz konusu olduğunda en önemli gelişme, Kemâleddin Fârisî'nin, İbn Havvâm'ın Fevâid'ine yazdığı Esâs adlı şerhte tüm Misâha kurallarını saf hendese açısından sıkı bir ispata tabi tutmasıdır; bu da Misâhayı sağın bir bilim olarak kurmak anlamına gelir. Benzer biçimde aynı esere Îzâh adlı başka bir şerh yazan İmâduddin Kâşî de aynı kuralları adedî olarak ispatlar. Misaha açısından diğer bir gelişme Semerkand'da vukû bulur: Cemşîd Kâşî, Miftâh'ının dördüncü makalesini Misâhaya tahsis eder ve tüm İslam matematik tarihindeki en ayrıntılı incelemeyi yapar; ayrıca aynı makalenin dokuzuncu babını binaların ve mimarî eserlerin misâhasına ayırır. Bu bölümün Mimar Sinan örneğinde görüleceği üzere, İslam medeniyetinde mimarî hendeseye, özellikle camii gibi büyük ölçekli binaların matematiksel çözümlemesine etkisi son derece açıktır. Misâha konusunda İstanbul'da müellifi meçhul bir yazarın kaleme aldığı el-İknâʻ fi ilmi'l-misâha adlı eser yanında en ayrıntılı incelemeleri Abdulmecîd Sâmûlî, er-Risâletu'l-nâfia fî'l-hisâb ve'l-cebr ve'l-misâha adlı eserinin üçüncü kısmında, İbn Hamza ise Tuhfe adlı eserinin dördüncü makalesinde yaparlar. Misâha tarihi açısından diğer bir gelişme olarak, XVI. yüzyıldaki Türkçeleştirme hareketine paralel olarak Emrî Çelebî, Mecmaʻu'l-garâîb fî'l-misâha adlı hacimli bir eser kaleme alır; ayrıca misaha büyük ölçekli muhâsebe matematik metinlerinde de Türkçe olarak işlenir.

İbn Heysem'den sonra Optik alanında, felsefî açıdan, İbn Rüsd'ün ve Fahreddin Râzî'nin çalışmalarında dikkate alınsa da, teknik içeriğine ilişkin yeni çalışmalar Tebrîz'de Kutbuddin Şîrâzî ve öğrencisi Kemâleddin Fârisî eliyle başlar. Fârisî, İbn Heysem'in Kitâbul'-menâzır'ını güncellemekle kalmaz, aynı zamanda gökkuşağının ilk matematiksel tasvirini verir; ayrıca kırılma açılarını adedî olarak ifade etmeye çalışır ki, onun bu yaklaşımı doğanın bilgisinin nicelleştirilmesi açısından önemlidir. Fârisî, yine belki de ilk defa olarak, optik konusunda ders kitabı hazırlar; bu, en azından Tebrîz Şenb-i Gâzân'da optik biliminin müfredata girdiğini gösterir. Bu geleneğin devam ettiğini en iyi Semerkand okulunun mensuplarının yazdığı eserlerden takip etmek mümkündür. Ali Kuşçu'nun ve Fethullah Şirvânî'nin çalışmaları Optik biliminin başta Astronomi olmak üzere, Matematik bilimlerinin doğal bir parçası haline geldiğini gösterir. İstanbul'da ise Hocâzade, Kutbuddin Muhammed, Hasan Dihlevî gibi bilginlerin çalışmaları ile birleşen bu araştırmalar nihâyet Takiyeddin Râsıd ile birlikte İslam medeniyetindeki son önemli, Kitâb nûr hadakati'l-ebsâr ve nûr hadîkati'l-enzâr adlı Optik kitabının telifi ile neticelenir.

Klasik dönemde İbn Halef Murâdî'nin Endülüs'te ve Ebû'l-İzz Cezerî'nin Anadolu'daki telifleriyle mekanik bilimi belirli bir olgunluğa erişmişti. Tahrîr döneminde bu konudaki çalışmalar daha çok Semerkand ve İstanbul havzalarında yoğunlaştı. Nitekim mekanik bilimi, Ali Kuşçu'nun günümüze gelmeyen et-Tezkire adlı çalışması yanında Alâaddin Kirmânî'nin kısmen Cezerî'nin kitabının tercümesi olmakla birlikte yeni eklemlerle zenginleştirdiği Bedâyiʻu'l-aʻmel fî senâyiʻi'l-hiyel adlı eseri ile Takiyeddin Râsıd'ın kadîm anlamdaki hiyel sahasında kaleme aldığı ve klasik mekanik âletlerinin hendesî-mekanik yapılarını incelediği et-Turuku's-seniyye fî'l-âlâti'r-ruhâniyye adlı eseriyle zirveye ulaştı. Takiyeddin, ayrıca mekanik-otomatik saatleri İslâm ve Osmanlı dünyasında ilk defa olarak ele alan el-Kevâkibu'd-durriyye fî vadʻi'l-benkamâti'd-devriyye adlı bir eser yazdı ve eserinde mekanik saatlerden, bunların çeşitlerinden ve yapımlarından bahsetti. Mekanik alanındaki tüm bu çalışmaların nazarî bir çerçevede kalmadığını ve Saray'da belirli bir uygulama alanı bulduğunu, Sultan III. Murad döneminde Cezerî'nin Hiyel'inin meçhul bir zanaatkâr tarafından Türkçe'ye çevrilmesi göstermektedir.

Bu dönemde belirsiz denklemler pek çok matematikçi tarafından ele alınmıştır. İzzuddin Zencânî, İbn Havvâm ve İbn Hamza bu matematikçilerin başında gelir. İbn Havvâm söz konusu olduğunda tarihî açıdan son derece ilginç bir durum ortaya çıkar: İlk defa bir matematikçi çoğunluğu belirsiz denklemlerden oluşan otuzu aşkın çözümsüz denklemi daha sonraki nesillerin çözmesi için bir araya getirir. Bilgide geleceğe yönelik 'ilerleme' ya da daha hafif bir deyişle 'gelişme' inancı, yukarıda işaret edilen tahkîk ve tahrîr yöntemlerindeki bilginin tarihsel bir varlık olarak idrak edilmesiyle son derece ilgilidir ki, "bugünkü bilgi geçmişe göre geliştiyse yarınki bilgi de bugüne göre gelişebilir, hatta gelişecektir" inancına dayanır. Öte yandan kombinatör analiz konusunda Merağa'dan Nasirüddin Tûsî, Tebriz'den Kemâleddin Fârisî, Mağrib'ten de İbn Bennâ öne çıkarlar. Tûsî'nin çalışmalarında, felsefî bir sorun olan sudûr nazariyesini kombinatör analiz yöntemiyle ispat etme kaygısı merkezîdir.

Mikdârî sayılar nazarîyesi konusunda Merağa'da, Tebrîz'de ve Tokat'ta tahrîr edilen, başta Tahrîru usûli'l-hendese ve'l-hisâb ile el-İkmâl olmak üzere tüm hendese eserlerindeki bilgiler güncellenmiştir. Ancak adedî sayılar konusunda, Tûsî'nin çalışmaları dışında, en önemli ilerleme Tebrîz'de Kemâleddin Fârisî tarafından gerçekleştirildi. Dost sayıları incelediği risalesinde Fârisî, asal sayılar üzerinden aritmetiğin temel teoremini formüle etti; faktörel ve kombinatör yöntemler hakkında yeni düşünceler geliştirdi; ayrıca figüratif sayılar üzerinde durdu.

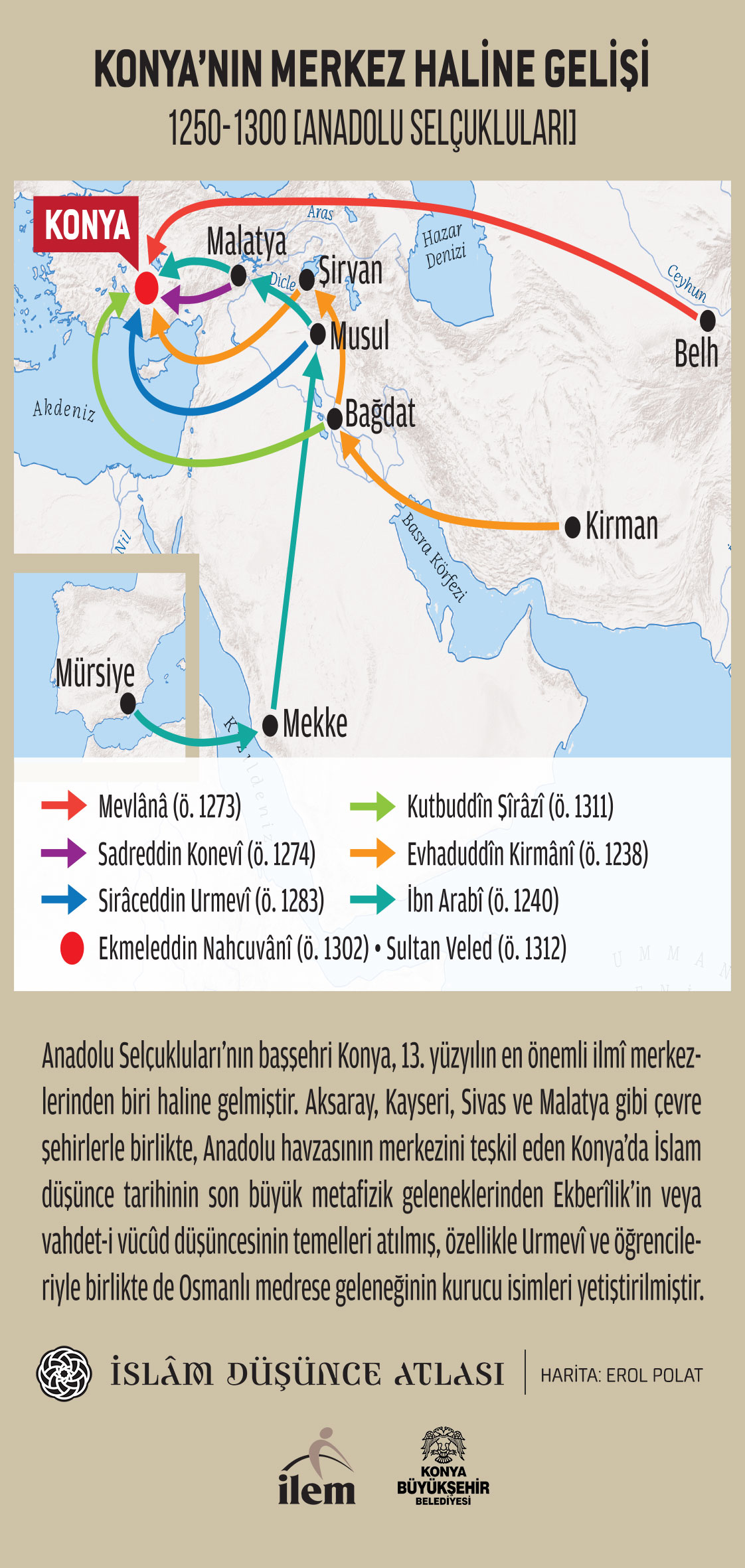
Tahrîr dönemi, en önemli ve çığır açıcı eserlerini Astronomi alanında verdi. Klasik dönemde ilmu'l-hey'et'e son şeklinin verilmesi, İbn Heysem'in doğa felsefesi ile matematik birlikteliği vurgusu, Harakî ve öğrencilerinin bu çizgiyi öne çıkartıp müfredata katması, Sultan Melikşah ve Sencer dönemlerinde kurulan rasathanelerde yapılan yeni gözlemler, tüm bunlar önce Harzemşahlar akabinde de Moğollar döneminde önce Merağa'da akabinde de Tebrîz'de bir araya getirilip büyük ilerlemelere kapı araladı. Çizilen resmin daha iyi idrâk edilebilmesi için iki örnek verilebilir: Alâaddin Harzemşâh'ın baş-astronomu Hüsâmeddin Sâlâr, daha sonra, önce Cengiz Hân'ın akabinde de İran'da İlhanlı hükümdarı Hülagu'nun baş-astronomudur. Harakî çizgisinin velût yazarı Şemseddin Çağmînî, Mesûd Kazerûnî'nin hocası iken, Kazerûnî de kendi oğlu, Merağa okulunun mensubu, Sivas Gök-Medrese'nin baş-hocası ve Tebrîz Şenb-i Gâzân matematik-astronomu okulunun kurucu ismi Kutbuddin Şîrâzî'ye hocalık yapmış; böylece bir eğitim-öğretim geleneği nesiller arası aktarıma sokulmuştur. Nitekim, Çağmînî'nin Mulahhas'ının hem Merağa'da hem de Tebrîz'de temel ders kitabı olması böyle bir sürekliliğin sonucudur.

Tüm bu birikim daha XIII. yüzyılın ilk yarısının sonuna doğru klasik Batlamyus astronomisinde re-form ihtiyacını doğurdu; bu ihtiyacı gidermek için yapılan çalışmalar, klasik dönemde oldukça nâdir görülen, gezegenler teorisinde yeni kinematik-geometrik modellerin teklif edilmesine yol açtı; bunun için matematik tekniklerde ilerlemeler kaydedildi; ayrıca bu modelleri gerçekleyecek rasatlar yapıldı. İlk tekliflerden biri Şâm kökenli olan, daha sonra Merağa'da Tûsî ile birlikte çalışan Mueyyeddin Urdî'den geldi; Urdî iddialarını Kitâb fî ilmi'l-hey'e adlı eserinde temellendirdi. İkinci ve etkili teklif bizzât Tûsî tarafından yapıldı. Tûsî, Merağa'dan önce başladığı çalışmalarını öncelikle el-Risâletu'l-muʻîniyye fî ilmi'l-hey'e'de Farsça olarak dile getirdi; akabinde Hall-i muşkilât-i muʻîniyye'de görüşlerini geliştirdi; Tahrîru'l-Macestî'ye ekledi; en nihâyet et-Tezkire fi ilmi'l-hey'e adlı Arapça eserinde son halini verdi. et-Tezkire astronomi tarihinde kendinden sonra en etkili eserlerden biri oldu, üzerine şerhler, hâşiyeler ve talikâtlar yazıldı; ders kitabı olarak kullanıldı. Merağa okulunun diğer bir mensubu Muhyiddin Mağrîbî benzer çalışmaları sürdürdü; Kutbuddin Şîrâzî ise Sivas Gök-Medrese'de belki de modern öncesi dönemin en önemli iki astronomi kitabını, Nihâyetu'l-idrâk fî dirâyeti'l-eflâk ve et-Tuhfetu'ş-şâhiyye fi ilmi'l-hey'e adıyla kaleme alarak Urdî, Tûsî ve Mağrîbî'nin düşüncelerini geliştirdi. Tebrîz'de Şenb-i Gâzân'da Merağa'nın geliştirdiği modeller müfredata dahil edildi; yalnızca İslâm coğrafyasına mensup öğrencilere değil Gregory Choniades örneğinde olduğu üzere Bizanslı tâliblere de öğretildi ve Batı dünyasına aktarıldı. Daha önce de Tûsî'nin oğlu Asîluddin Hasan döneminde Merağa'daki astronomlarla birlikte çalışan Çinli astronom Fao-mun-ji ile İslam ve Çin astronomi gelenekleri arasında bir irtibat kurulmuştu.

Astronomide, bahusus gezegenler teorisindeki yeni arayışlara en önemli katkılardan biri de, esasen daha çok pratik karakteri ile bilinen Şâm - Kâhire havzasından geldi. İbn Şâtır, bizzat Şâm'da yaptığı gözlemlerden hareketle Nihâyetu's-sûl fî tashîhi'l-usûl adlı eserinde yeni gezegenler teorisini dizgeli bir biçimde dile getirdi; daha fazla episaykil kullanarak eksantrik ve ekuant kavramlarını tasfiye etti. İbn Şâtır'ın modelleri matematiksel açıdan Kopernik'in modelleriyle eş-değerdir. İbn Şâtır'ın yaklaşımları kendinden sonra fazla karşılık bulmasa da, Seydî Ali Reis'in XVI. yüzyıldaki Matematik bilimlerdeki Türkçeleştirme akımına uygun olarak kaleme aldığı Hulâsatu'l-hey'e adlı Türkçe ilk teorik astronomi kitabında kısmî olarak dikkate alındı. Ancak bu konudaki en köktenci yaklaşım yine Şâm-Kâhire havzasına mensup olan, daha sonra İstanbul'a gelen İbn Nakîb'e aittir. O, Tenbihu'n-nukkâd alâ-mâ fî'l-hey'eti'l-meşhûre mine'l-fesâd adlı risalesinde Batlamyus, Tûsî ve Şirâzî'nin Astronomi sistemlerini eleştirerek hepsini birden 'eski', 'yaygın' Astronomi olarak adlandırır ve yerlerine İbn Şâtır Astronomisini 'yeni astronomi' olarak teklif eder. Hemen ifade edilmelidir ki, klasik astronominin sınır-soruları her zaman bilginlerin dikkatini çekmiştir; örnek olarak Mîrim Çelebî, Ahaveyn ve Seydî Ali Reis İstanbul'da, Giyâseddin Deştekî ise Şîrâz'da bu tür sorunlarla uğraşmıştır. Batlamyus astronomisine daha köktenci bir eleştiri daha önce Semerkand okulu mensubu Ali Kuşçu tarafından gelmiş; gerçekliğe mutâbık bir astronomi için Meşşâî felsefenin metafizik ve fizik ilkelerinden kurtulmak gerektiğini ileri sürmüş ve bu düşüncelerini temsilen el-Fethiyye fî ilmi'l-hey'e adlı eserini İstanbul'da yazarak Fatih Sultan Mehmed'e ithaf etmiştir. İstanbul Rasadhanesi'nin kurucusu Takiyeddin Râsıd ise mevcut astronominin teorik yapısında bir sorun görmezken matematiksel kesinliği artırmak için hem daha dakik gözlem yapacak yeni âletler icat etti; hem yeni matematik teknikler geliştirdi hem de ilk defa olarak mekanik-otomatik saatleri astronomik gözlemlerde kullandı. Tüm bunların neticesinde tarihte ilk defa olarak trigonometrik fonksiyon tablolarını ve zîc hesaplarını ondalık kesirlere göre düzenledi.

İslam medeniyetinde gözlem yaparak gök-yüzü haritaları yani 'zîc' hazırlama VIII. yüzyılın ikinci yarısının sonlarından itibaren başlayan ve devam eden bir gelenektir. Bu zîcler hem pratik hem de teorik nedenlerle son derece önemlidir çünkü takvim yapma, astrolojik ön-görme, parametrelerden harekete ederek yeni modeller geliştirme gibi pek çok konu zîclere bağlıydı. Klasik dönemde Bağdâd, Kâhire, İran ve Türkistan havzalarında kurulan pek çok rasathanede onlarca zîc hazırlanmış; daha sonra bu zîcler üzerine pek çok çalışma yapılmıştır. Tahrîr döneminde de devam eden bu süreçte İslam medeniyetinin en önemli zîcleri hazırlanmıştır denebilir. Merağa'da hazırlanan Zîc-i İlhânî, Tebrîz'de Şemseddin Vabkanevî'nin hazırladığı Zîcu'l-muhakkaki's-sultânî alâ usûli'r-rasadi'l-İlhânî; İbn Şâtır'ın hazırladığı ez-Zîcu'l-Cedîd, Semerkand'da hazırlanan Zîc-i Uluğ Bey, Kâhire'de hazırlanan Zîcu Ebî'l-Feth es-Sûfî, İstanbul'da hazırlanan Sidretu Muntehâ'l-efkâr fî Melekûti'l-feleki'd-devvâr (ez-Zîcu'ş-Şehinşâhî) ile Cerîdetu'd-durer ve harîdetu'l-fiker. Yukarıda da işaret edildiği üzere Cerîdetu'd-durer tarihte ondalık kesirlerin ilk kullanıldığı zîctir. Bu zîclerin bir kısmı daha sonraki astronomlar tarafından şerh edilmiş; farklı şehirlere uyarlanmıştır. Söz konusu dönemde en dikkati çeken şerhler Ali Kuşçu, Mirim Çelebî, İbn Ebî'l-Feth Sûfî ve Bircendî tarafından Zîc-i Uluğ Bey'e yapılmıştır.

Bu dönemde matematik bilimlerdeki önemli bir gelişme Mîkât biliminin (ilmu'l-mîkât=vakit tayini bilimi) bağımsız bir disiplin olarak kurulmasıdır. Kâhire-Şâm havzasında vuku bulan bu gelişme, Memlûk coğrafyasındaki Astronomi biliminin pratik karakteri ile de ilgilidir. Şemseddin Hâlîlî'nin en üst seviyede temsil ettiği bu disipline ilişkin eserler İstanbul'a intikal etmiş, Muhammed Konevî ve ardılı Mustafa b. Ali Muvakkıt'ın çalışmalarıyla Osmanlı mîkât geleneğinin ayrılmaz bir parçası halini almışlardır.

Tahrîr döneminde diğer bir gelişme astronomik âlet yapımının hem nicelik hem de nitelik olarak karmaşıklaşması ve bir tür bağımsız ilmî disiplin hâlini almasıdır. Burada bahsedilen âletler basit anlamıyla Merağa, Tebrîz, Semerkand ve İstanbul gibi rasathanelerde kullanılan büyük-ölçekli âletler değildir; tersine kastedilen günlük yaşamda uzman bir astronomdan tahsilli bir insana kadar farklı insanların vakit tayini, mesafe vb. işlemler için kullanabileceği onlarca farklı âlettir. Bu konudaki en önemli isim hiç şüphesiz, Hasan Merrâkûşî'nin Kâhire'de kaleme aldığı ve kendinden sonraki tüm literatürü etkileyen Câmiʻu'l-mebâdî ve'l-ğayât fî ilmi'l-mîkât adlı çalışmasıdır. Pratik karakteri ağır basan ve mîkât ilmini kuran bir geleneğe sahip Şâm - Kâhire havzası astronomi aleti, yapımı, yeni âlet icadı ve bu konuda muhtelif eserler yazma açısından tüm İslam medeniyeti tarihi içinde özel bir dikkati hak eder. Onlarca âlimin kaleme aldığı ve yüzlerce nüshaları bulunan eserler tüm İslam coğrafyasında yaygın olarak kullanılmıştır. Söz konusu âletler basit günlük kullanım için imal edildiği gibi, karmaşık astronomi teorilerini tersim etme ve uygulanabilirliğini gösterme maksadıyla da yapılırdı. Şâm - Kâhire hattı en iyi karşılığını İstanbul'da buldu; Muhammed Konevî bağlantıyı kurdu, Mustafa Muvakkıt zirveye taşıdı. O kadar ki, XVI. yüzyılın Türkçeleştirme amacına bağlı olarak astronomi âletlerine ait hazırladığı otuzu yakın Türkçe eser XIX. yüzyıla kadar tüm İslam coğrafyasında kullanıldı.

Bu dönemin en önemli başarılarından biri de matematiksel coğrafya ve deniz astronomisi konularındaki ilerlemelerdir. Kaynağını klasik dönem çalışmaları ile Endülüs-Mağrib havzasında bulan bu çalışmalar İbn Mâcid ve Süleyman Mehrî ile en önemli eserlerini verdi. Söz konusu çizgi İstanbul'da Pîrî Reis ve Seydî Âli Reis ile denizcilik; Mustafa Muvakkıt ile matematiksel coğrafya konularında devam ettirildi.

Tahrîr döneminde en önemli konulardan biri yine matematik nesnelerin ontolojisi ve doğaya ilişkin matematiksel bilginin meşrûiyeti olmaya devam etti. Nefsu'l-emr kavramı üzerinden yürütülen bu tartışmalar, XIII. yüzyılın ikinci yarısında Nasirüddin Tûsî ve Şemseddin Kîşî ile başlayıp Ali Kuşçu, Celâleddin Devvânî, Taşköprülü-zâde gibi isimlerle XVI. yüzyılın sonuna değin sürdü. Bu konuda kanonik çerçeveyi XIV. yüzyılın ilk yarısında Semerkand matematik-astronomi okulunun zihniyeti çerçevesinde Seyyid Şerîf Cürcânî çizdi ve onun görüşleri asırlarca tartışıldı. Bu çerçevede tartışılan diğer bir sorun, doğadaki herhangi bir olgu ve olaya ilişkin bilgide 'innî delili' (olgu merkezli açıklama) veren matematik ile 'limmî delili' (neden merkezli açıklama) veren doğa felsefesi arasındaki ilişkinin neliğiydi. Nasirüddin Tûsî'nin et-Tezkire fî ilmi'l-hey'e adlı önemli eseri ve şerhleri üzerinden yürüyen bu tartışma, doğa ile matematiksel bilgi arasındaki ilişki hakkında olduğu kadar aynı zamanda mantığın bir matematiksel-doğa bilimine uygulanması açısından da iyi bir örnektir. Diğer bir sorun ise özellikle astronomide kinematik-geometrik modellerin, güneş ve ay tutulmalarında olduğu gibi, şimdi yanında geçmiş ve gelecek hakkında verdiği bilgilerin dakikliği ve epistemolojik meşrûiyetinin ne olduğu tartışmalarıydı. Yine Nasirüddin Tûsî'nin et-Tezkire fî ilmi'l-hey'e'si ve şerhleri üzerinden sürdürülen bu tartışma, Seyyid Şerif tarafından İşrâkî felsefede Sühreverdî'nin öne sürdüğü hads kavramı etrafında çözülmeye çalışıldı. İstanbul'da ise Molla Hüsrev, kinematik-geometrik modellerin içinde yapılan hesaplarla daha önce rasat edilmemiş durumları ön-görme ve gözlemlerden elde edilen bazı küçük değerlerin modeller idealize edilirken dışarıda bırakılmasına rağmen modellerin gerçekliğe mutabakatının devam etme sorunlarını tartıştı. Tam burada şu noktaya da dikkat çekilmelidir: Matematikçi filozofların talepleri, İşrâkî felsefenin matematikleştirmeye uygun mikdârî ontolojik-birim anlayışı, nefsu'l-emr tartışmaları gibi konular, Kutbuddin Şîrâzî'yi Nihâyetu'l-idrâk'inde başta astronomi olmak üzere matematik bilimleri fizik ve metafizikten daha değerli bilimler olarak görme iddiasına kadar götürmüştür. Sivas'ta dile getirilen bu düşünceler Tebriz'de de devam ettirilmiş, bu da doğal olarak, Meşşâî ve kelâmî çizgideki düşünürlerin eleştirilerini davet etmiştir.